[QSP / QSVT] QSVT 應用：AA

2023 iThome 鐵人賽

DAY 16

自我挑戰組

不嚴謹的量子計算雜談系列第 16 篇

15th鐵人賽量子計算

bwl

2023-09-25 08:46:51

219 瀏覽

分享至

原來 QSVT 也可以應用在振幅放大？讓我們一探究竟吧！

$A = |t\rangle\langle t|s\rangle\langle s|$

為目標矩陣，也就是說，我們要用多項式轉換 $A$ 的奇異值： $\langle t|s\rangle$ ！什麼樣的函數可以讓大於 $0$ 的實數變成 $1$ ？沒錯，就是昨天提到的 $\Theta(x)$ ：

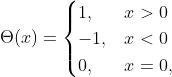
在此我們將 $\Theta(x)$ 稱為 sign 函數。還記得在 Block-Encoding 有提到，被編碼的矩陣 $A$ 不見得要在「左上角」， $A$ 可以在任意位置。推廣的 block encoding 稱為 projector unitary encoding：指定兩個正交投影算子 (orthogonal projector) $\tilde\Pi$ 和 $\Pi$ ，若

$A = \tilde\Pi U\Pi,$

我們說么正矩陣 $U$ 是 $A$ 的 projector unitary encoding (在 QSVT 定理處可發現一些端倪)。在這裡， $\tilde{\Pi} = |t\rangle\langle t|$ 、 $\Pi = |s\rangle\langle s|$ ，而 $U=I$ ！經過 QSVT 之後，

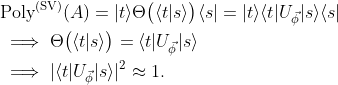
整個計算過程可以歸結成以下步驟：

準備初始量子態 $|s\rangle$
應用 (apply) $U_{\vec\phi}$ 在 $|s\rangle$ 上
此時測量到目標量子態 $|t\rangle$ 的機率接近 $1$ ，完成！

值得注意的是，在 QSVT 過程中，我們不斷使用到 $\Pi=|s\rangle\langle s|$ ；也就是說，除非 $\Pi$ 可以 oracle 的方式存取，否則我們需要很多 $|s\rangle$ ，因此此處的 AA 並不 oblivious！幸運的是，由於我們使用的是 sign 函數，於是舒芙蕾問題不會發生，因此這是 fixed-point AA！(經過某些修改，利用 QSVT 的 AA 可以是 oblivious + fixed-point。)